[논문 리뷰] Horizon Reduction Makes RL Scalable

논문 정보

제목: Horizon Reduction Makes RL Scalable

저자: Seohong Park, Kevin Frans, Deepinder Mann, Benjamin Eysenbach, Aviral Kumar, Sergey Levine. UC Berkeley.

학회: NeurIPS 2025 (Spotlight)

링크: https://arxiv.org/abs/2506.04168

Overview

Target task: Offline Goal-conditioned RL (GCRL)
Algorithm class
- Policy learning: Hierarchical flow BC policy
- Value learning: $n$-step SARSA
Motivation
1. 데이터의 개수가 늘어날수록 또는 모델의 크기가 늘어날수록 네트워크의 성능이 높아진다는 일반적인 기대와 다르게 offline RL의 경우 그렇지 않다.
2. 특히, 복잡한 task일수록 그리고 긴 horizon의 task일수록 offline RL의 성능이 데이터 양이나 모델의 크기에 scale하지 않는다.
Solution: Horizon이 길어서 발생하는 문제를 알아보고 해결하자
1. Value learning using $n$-step SARSA
2. Hierarchical policy learning

Experiment Setup

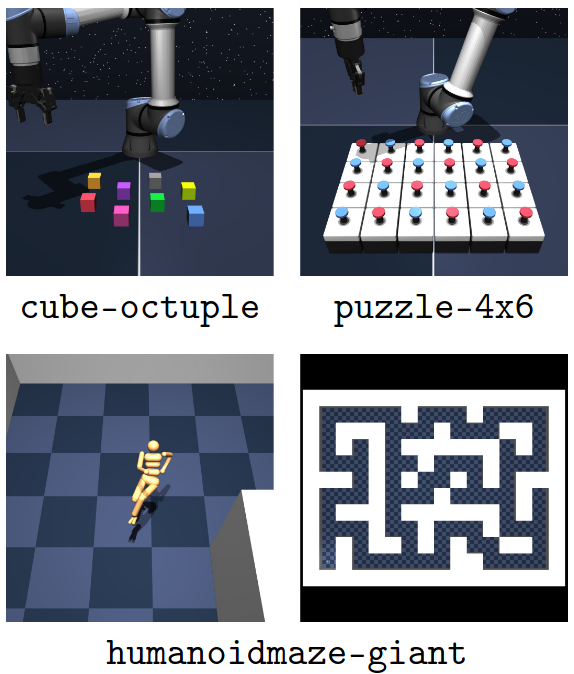
Environments: OGBench에서 challenging한 4개 tasks 사용
- cube-octuple, puzzle-{4x5, 4x6}, humanoidmaze-giant
- 지금까지 offline GCRL 방법론들이 1M transitions 데이터셋으로는 제로 성능을 벗어나지 못하는 tasks

Task-agnostic dataset

각 domain마다 task-agnostic하게 1B (10억) transitions 수집

Each requires 1000-1500 CPU hours and 279-551GB of disk space

Task-agnostic? [링크]

Evaluation 환경은 풀고자 하는 task가 정해져 있음
- e.g., Cube 환경: Cubes들을 정해진 순서대로 정해진 위치에 pick & place
- e.g., Puzzle 환경: 특정 모양의 puzzle이 되도록 button을 누르며 색을 바꿈
- e.g., Maze 환경: 특정 위치에 도달
풀고자 하는 task를 모른 채로 scripted policy를 사용하여 데이터 수집 (*-play dataset)
- e.g., Cube 환경: 아무 cubes들을 아무 데나 pick & place하며 수집
- e.g., Puzzle 환경: 아무 버튼이나 막 누르면서 수집
- e.g., Maze 환경: random하게 navigate하며 수집
따라서 데이터셋은 보상 (goal 달성 여부)이 없는 $(s,a)$ pairs로 구성
- $\mathcal{D} = \lbrace \tau^{(n)} \rbrace_{n=1}^{N}$, $\tau=(s_0, a_0, s_1, a_1, \ldots, s_H)$.

Idealization: Offline GCRL의 다른 challenging 요소를 최대한 배제

Low-dimensional state-based observations (not visual observations)
Oracle goal representations (e.g., 단순 좌표 뿐만 아니라 로봇 state 등도 포함)
Out-of-distribution evaluation goals 제거
데이터셋의 충분한 coverage와 optimality 확보

Baseline algorithms: IQL, CRL, SAC+BC, Flow BC

Standard Offline RL Methods Struggle to Scale

기존 Offline RL 알고리즘의 성능은 데이터 수에 scalable하지 않는다.

Batch size 1024로 5M gradient steps 학습 / MLP 구조: (1024, 1024, 1024, 1024)

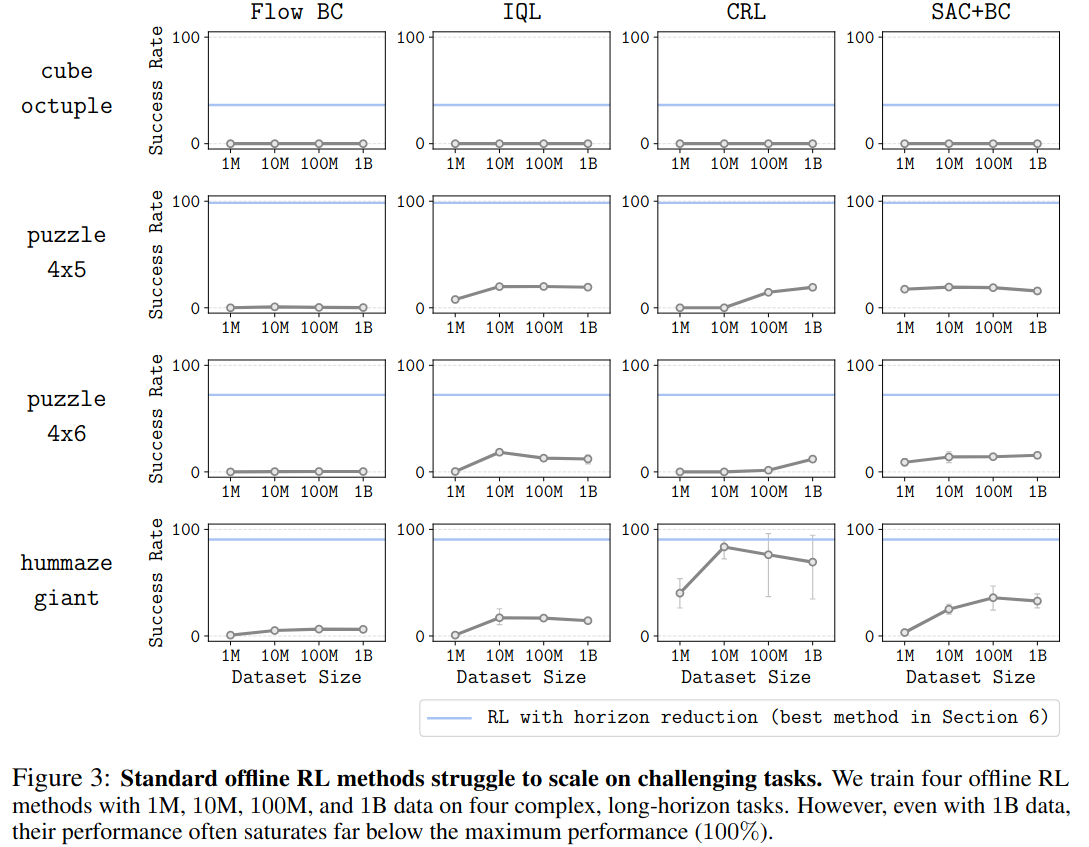
기존 Offline RL 알고리즘의 성능은 모델 크기에 scalable하지 않는다.

SAC+BC를 1B 데이터셋에 대해 학습

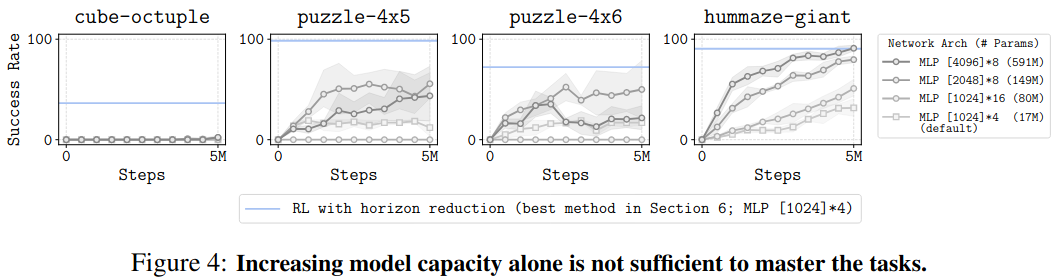
The Curse of Horizon

In Value Learning

Hypothesis

TD learning을 사용하여 $Q$ 함수를 학습할 때, TD target인 $r_t + \gamma Q_\theta (s_{t+1}, a_{t+1})$ 에 bias가 있으며, 이 bias는 horizon을 따라 누적되어 더 큰 bias를 만든다.
Bias의 원인: 실제 Bellman equation에 등장하는 $\mathbb{E}_{s’ \sim p(\cdot \mid s, a), a’\sim\pi(\cdot\mid s’)}[Q^{\pi}(s’, a’)]$ 텀에서 기댓값 대신 sample $(s’, a’)$을 사용하기도 하고, 실제 action value가 아닌 $Q$ network를 bootstraping하기 때문에 bias는 존재할 수 밖에 없다.
“Biases accumulate over horizon” ⇒ reward signal과 먼 $(s_t, a_t)$까지 TD backups이 전달되어 오는 데 biases가 누적됨
- $Q_\theta(s_{H}, a_{H})\rightarrow Q_\theta(s_{H-1}, a_{H-1}) \rightarrow Q_\theta(s_{H-2}, a_{H-2})\rightarrow \ldots \rightarrow Q_\theta(s_{t+1}, a_{t+1}) \rightarrow Q_\theta(s_{t}, a_{t})$

Empirical evidence

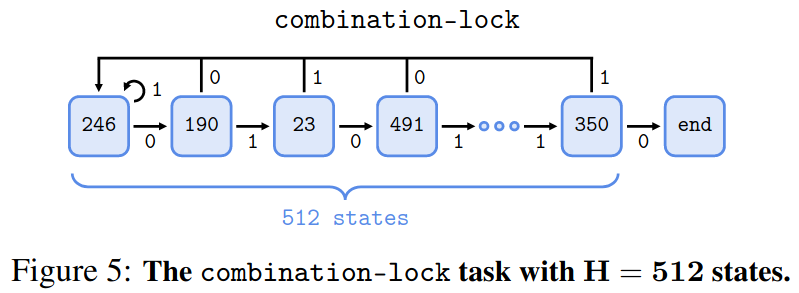
Environment: combination-lock
- 1부터 $H$까지의 숫자가 랜덤하게 배열되어 첫 번째 state부터 마지막 state까지 구성
- 각 state의 표현형은 $\log_2 H$ 차원의 binary vector (이진법)
- 각 state마다 0과 1중 랜덤하게 correct action, incorrect action을 할당
- 한 state에서 correct action을 하면 다음 state로 넘어가고, incorrect action을 하면 첫 번째 state로 돌아가는 환경
- 마지막 state에 도착하면 0의 보상을 받고 그 외에는 -1 보상을 받음
Datasets
- 1-step dataset: 모든 $2 \times H$ 개의 $(s,a)$ pair에 대해 보상 값과 다음 상태를 적어준 데이터셋 ${(s,a,r,s)}$ ( **)
- $n$-step dataset: 각 state 마다 50%의 확률로 $n$ step 동안 correct actions 했다고 가정하고 $n$-step transition $(s_t, a_t, \sum_{k=1}^{n} r_{t+k}, s_{t+n})$ 또는 나머지 50%의 확률로 incorrect actions 했다고 가정하고 $n$-step transition
- 즉, 두 데이터셋 모두 reward signal을 포함하고 있음
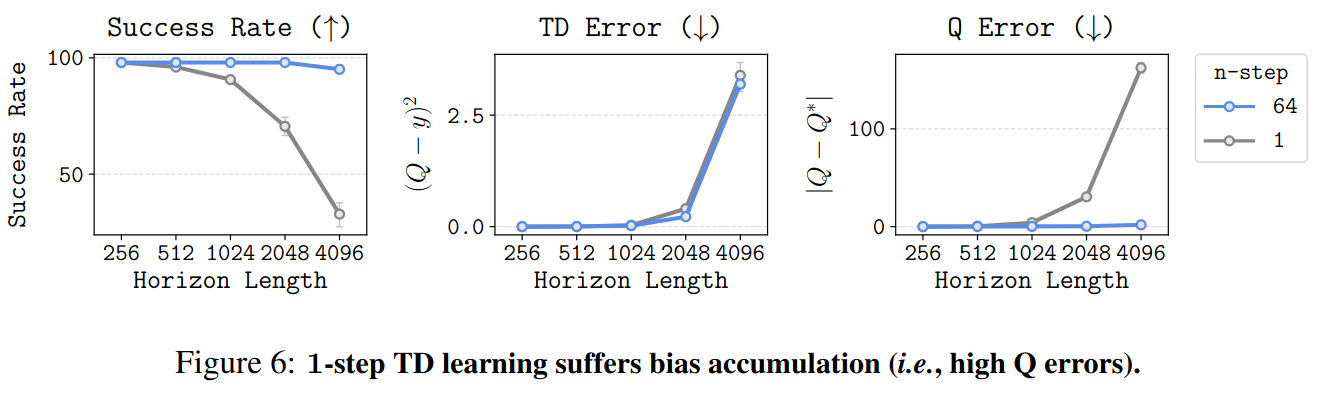
Results: 1-step DQN과 $n$-step DQN ($n=64$)을 데이터셋으로 학습시키고 성능을 비교
- 환경의 상태 개수이자 horizon인 $H$가 증가할수록 1-step DQN의 success rate가 떨어짐
- TD error는 비슷하지만, 1-step DQN의 $Q$ error ($Q^{\pi} - Q_\theta)$는 horizon이 길어질수록 급격히 증가
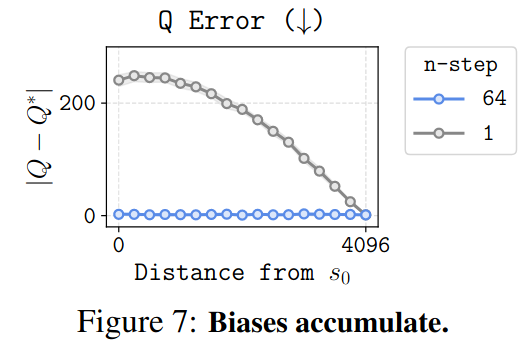
- Horizon이 길수록 biases가 커진다는 empirical evidence: $H=4096$일 때, 각 state에서 $Q$ error를 구해본 결과 terminal state와 멀수록 $Q$ error가 컸음
- 1-step DQN의 경우 하이퍼파라미터 조정을 해도 curse of horizon이 해결되지 않음

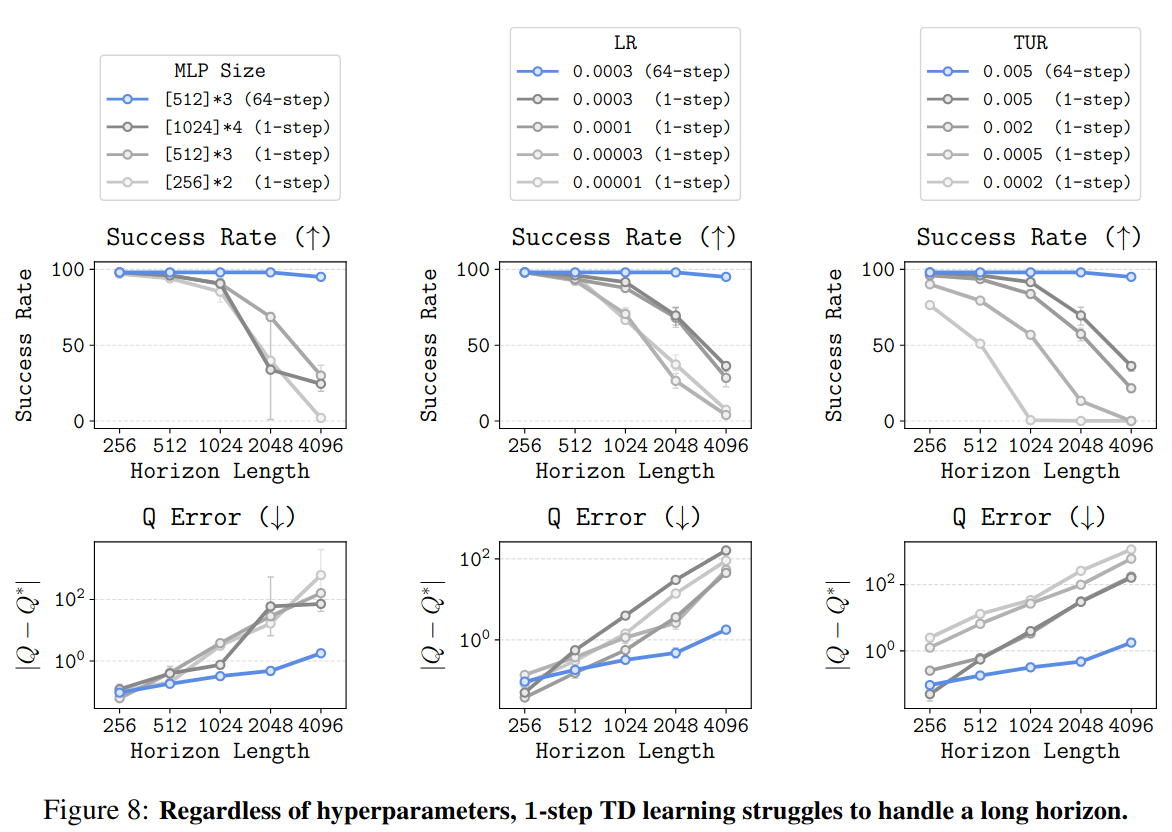
In Policy Learning

Horizon이 길수록 상태 $s$에서 action-value 값이 가장 높은 행동 $a$를 mapping하는 policy learning이 어려워진다.
- 말로 이렇게만 써있어서 공감하기 어려웠음
Value learning에서 $n$-step returns 비슷한 역할을 할 수 있는 방법론으로 hierarchical policy가 있음
- $\pi(a \mid s, g)$ ⇒ $\pi^h(w \mid s, g)$ + $\pi^l(a \mid s, w)$
- High-level policy $\pi^h(w \mid s, g)$는 subgoal $w$를 출력
- Low-level polict $\pi^l(a \mid s, w)$은 subgoal 달성을 위한 행동 $a$를 출력

Horizon Reduction Makes RL Scale Better

$n$-step SAC+BC: value learning에 $n$-step return을 사용하는 것이 curse of horizon을 완화할 수 있다는 것을 보이기 위해 $n$-step SAC+BC를 실험에 포함
Hierarchical flow BC / HIQL: policy learning에 hierarchical policy를 사용하는 것이 curse of horizon을 완화할 수 있다는 것을 보이기 위해 hierarchical flow BC와 HIQL을 실험에 포함
SHARSA: n-step return과 hierarchical policy를 사용하여 curse of horizon을 더 많이 완화할 수 있는 이 논문에서 제안하는 알고리즘

Learning a high-level policy and low-level policy

High-level policy

Offline RL에서 많이 사용되는 policy learning 방법론인 TD3 + BC의 경우 보통 다음을 최대화하도록 $\pi_\phi$를 훈련 (reparameterization) $Q_\phi(s, a^{\pi_\theta}), \text{ where }\, a^{\pi_\theta}\sim \pi_\theta(a\mid s).$

하지만 action이 아닌 subgoal의 경우 discrete 할 수 있는 등의 이유로 subgoal $w^{\pi_\theta} \sim\pi_\theta^{h}(w\mid s, g)$을 샘플링하여 $Q_\phi$ network를 미분하는 $\nabla_\theta Q_\phi(s, w^{\pi_\theta},g)$ 계산이 doesn’t make sense할 수 있다.

따라서, 먼저 $Q$ network를 사용하지 않고 behavior cloning을 이용하여 high-level BC policy $\pi_\beta^h$를 학습.
- 기본적으로 $n$-step transition $(s_h, a_h, \ldots, s_{h+n})$을 사용하고 subgoal $w=s_{h+n}$으로 설정하여 학습
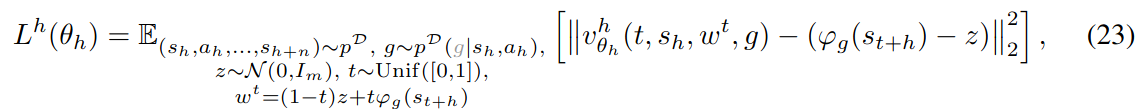
Rejection sampling을 사용하여 $Q_\phi$ network까지 고려하는 high-level policy $\pi^{h}$ 추출
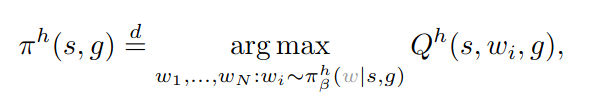
이때, $Q^{h}$ 는 high-level SARSA 학습 방법으로 학습됨

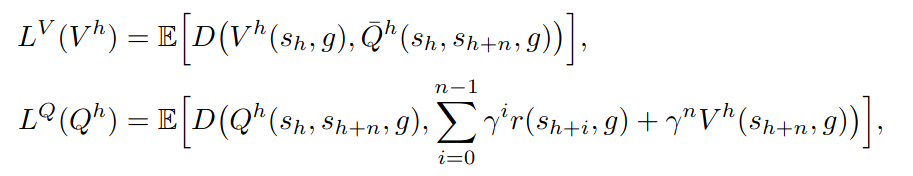
Low-level policy

그냥 일반적인 goal-conditioned flow BC로 학습 ⇒ SHARSA
High-level policy learning 때 학습했던 것처럼 또 다른 SARSA + rejection sampling 사용 ⇒ Double SHARSA